Vamos a ver lo que es una relación en el sentido matemático. Se trata de un concepto sencillo y fundamental a partir del cual se construye buena parte de la matemáticas. Este artículo trata de las relaciones binarias.





Inicio
Suponiendo que disponemos de dos conjuntos E y F definir una relación R entre E y F es darse un subconjunto del conjunto ExF llamado "grafo de R".
En esta definición, ExF designa el producto cartesiano entre E y F. Son todos los pares posibles (e,f) donde "e" es elemento de E y "f" elemento de F. Por lo tanto al definir una relación R entre E y F es elegir determinados pares (e,f), algunos si, otros no. Llamamos "grafo" y notamos GR el conjunto de los pares elegidos. Para un determinado par (e,f) la proposición "e R f" se cumple (es verdadera) si y solo si el par (e,f) pertenece al grafo de R:
\[Para\;G\subset R,\;\;\;\;\forall(e,f)\in E\times F,\;e\,R\,f\;\Leftrightarrow(e,f)\in G_{R}\]
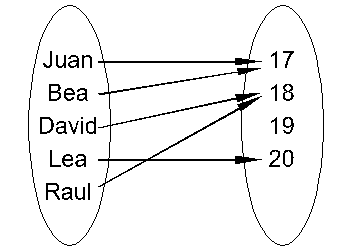
Antes de seguir, veamos un ejemplo. Sean E y F los conjuntos \(E=\left \{ Juan,Bea,David,Lea,Raul\right \}\) y \(F=\left \{ 17,18,19,20\right \}\). Por lo tanto,
\[\begin{align*}E\times F =&\{(Juan,17),(Juan,18),(Juan,19),(Juan,20)\\&(Bea,17),(Bea,18),(Bea,19),(Bea,20) \\&(David,17),(David,18),(David,19),(David,20) \\&(Lea,17),(Lea,18),(Lea,19),(Lea,20) \\&(Raul,17),(Raul,18),(Raul,19),(Raul,20)\}\end{align*}\]

Ahora voy a definir la relación Rg, que decido llamar "le gusta el número". Para ello se seleccionan algunos pares y otros no (también podría elegir ninguno o todos). Supongamos que elijo los pares: (Juan,18), (Juan,19) y (Bea,17), ahora puedo afirmar que "JuanRg18" es verdadera mientras que "LeaRg17" no lo es. Decimos que "Juan" y "18" estan relacionados y que "Lea" y "17" no lo estan. O en este caso que a Juan le gusta el número 18, y también el 19 mientras que a Lea no le gusta ningún número.
Relación funcional

La relación "le gusta el número" tiene muy pocas propiedades interesantes. Por lo tanto vamos a ver otra que sí tiene una propiedad interesante y es a relación "tiene la edad de". Suponiendo que Juan y Bea tienen 17 años, David y Raul tienen 18 y Lea 19, vamos a definir la relación Re que denominamos "tiene la edad de" a partir del subconjunto de ExF llamado "grafo de Re": GRe = {(Juan,17),(Bea,17),(David,18),(Lea,19),(Raul,18}. Esta relación tiene una peculiaridad que la hace interesante y es que todos los elementos de E estan relacionados como mucho con un elemento de F. Es decir que nadie tiene dos edades distintas. A partir de esta relación funcional es posible definir una función sobre el conjunto E a valores en F, que a cada elemento de E asocia como mucho un elemento F. Y esta es la definición de una función. Si la función se nota "f", "17" se nota "f(Juan)" y se llama "imagen de Juan", mientras "Juan" sería un antecedente de "17". El conjunto de los elementos que tienen una imagen se llama dominio de la función. Notese que en el dominio se habla de LA imagen de cada elementos porque siempre hay una sola, mientras que cuando lo hay, se habla de UN antecedente de un elemento de F porque podría haber otros. "17" tiene dos antecedentes, "20" no tiene ninguno. Una aplicación entre dos conjuntos E y F es una función para la cual todos los elementos de E tienen una imagen, es decir que se habla de una aplicación cuando el dominio de la función es E.

Hay evidentemente mucho mas que decir sobre las relaciones funcionales, se caracterizan por ejemplo las funciones o aplicaciones inyectivas, sobreyectivas, biyectivas etc. (ver artículo en sección de aplicaciones).
Relación sobre un conjunto
Tenemos una relación sobre un conjunto cuando E y F son el mismo conjunto. En este caso la relación relaciona elementos del conjunto entre sí. Es una caso muy habitual y en este caso podemos hablar de reflexividad, simetría, transitividad etc.
-


Ejemplo de relación sobre el mismo conjunto en el que no se aprecian propiedades tales como la reflexividad, simetría o transitividad.
-


Notese que la relación de igualación ("=") también llamada "identidad" es una relación sobre el mismo conjunto E cuyo grafo \(\Delta = \{(e,e)/e\in E\}\) es llamado diagonal de E:
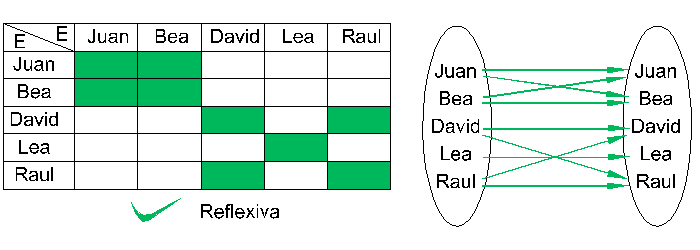
Relación reflexiva
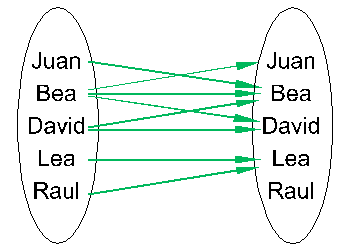
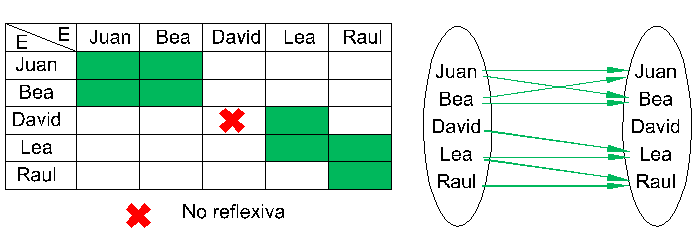
Supongamos que E=F trabajamos por lo tanto sobre el conjunto E. En este caso la relación es "reflexiva" significa que para cualquier "e" de E, resulta que "e" está en relación con él mismo: e R e. Por ejemplo, la relación "tiene la misma edad que" es obviamente reflexiva: Juan tiene la misma edad que... Juan! En cambio, la relación "quiere a" que notamos Rq definida por su grafo: GRq = {(Juan,Juan),(Juan,Bea),(Bea,Bea),(Bea,Juan),(David,Lea),(Lea,Lea),(Lea,Raul),(Raul,Raul)} no es reflexiva porque no todo el mundo tiene la autoestima suficiente como para quererse a sí mismo: David no se quiere a sí mismo.


Notese que decir que una relación es reflexiva es equivalente a decir que su grafo incluye la diagonal: \(\Delta \subset Gr\)
Relación simétrica
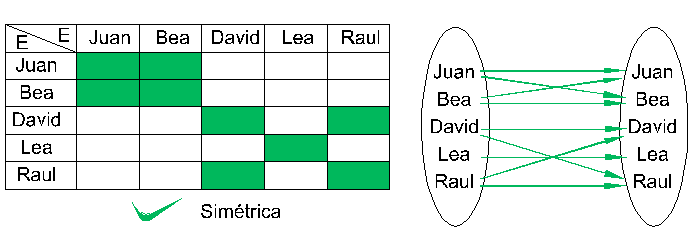
Sobre un mismo conjunto E, se dice de una relación que es simétrica si y solo si el hecho de que un elemento "e" está en relación con otro "f" conlleva que "f" está en relación con "e".
\[\forall(e,f)\in E^{2},\;e\,R\,f \Rightarrow f\,R\,e\]
Por ejemplo la relación "tiene la misma edad que" es simétrica, en efecto el hecho que Juan tiene la misma edad que Bea conlleva que Bea tiene la misma edad que Juan.
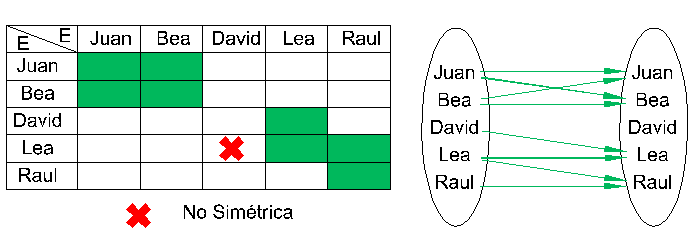
Desgraciadamente la relación "quiere a" no es simétrica: David quiere a Lea pero Lea no quiere a David. Son cosas de la vida.


Relación antisimétrica
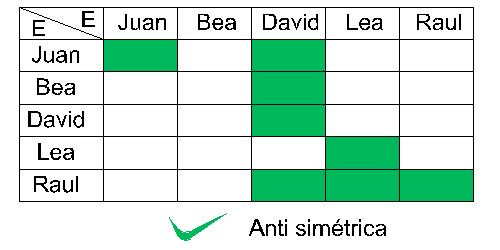
Sobre un mismo conjunto E, se dice de una relación R que es antisimétrica si y solo si podemos afirmar que no hay elementos e y f de E distintos entre si que esten en relación uno con el otro y viceversa (e R f y f R e). Formalmente, se dice que si dos elementos cumplen e R f y f R e, es que e=f:
\[\forall(e,f)\in E^{2}\;\;e\,R\,f\;y\;f\,R\,e\;\Rightarrow e=f\]


Sería poetico afirmar que la relación "quiere a" es antisimétrica. Estariamos diciendo que si fulano quiere a fulana y además fulana quiere a fulano entonces son una sola persona.
La relación "es menor o igual que" entre los naturales es una relación antisimétrica. Sean dos naturales e y f, si resulta que e\(\leq\)f y ademas f\(\leq\)e entonces e=f.
Relación transitiva
Sobre un mismo conjunto E, se dice de una relación R que es transitiva si y solo si el hecho de que eRf y fRg conlleva que eRg. Formalmente:
\[\forall(e,f,g)\in E^{3},\;\;eRf\;y\;fRg\;\Rightarrow\;eRg\]
La relación "tiene la mism edad que" es transitiva. Si Juan tiene la misma edad que Bea y Bea tiene la misma edad que Marco, entonces Juan tiene la misma edad que Marco.
La relación "es estrictamente menor que" definida sobre los naturales también es transitiva: 1<2 y 2<3, luego 1<3, y así para cualquier tripletes de naturales a,b,c, si a<b y b<c entonces a<c.
En cambio la relación "quiere a " no es transitiva.

Nota: La transitividad es un asunto particularmente interesante porque la mente humana tiende a pensar que las relaciones de nuestro entorno son todas transitivas y muchas de ellas que se dan por transitivas... ¡No lo son! Y suele costar admitirlo. Asi pues el hecho que una cosa A sea mejor que una cosa B la cual a su vez es mejor que una cosa C nos suele llevar a pensar que A es un chollo, C un desastre y pensamos que A es francamente mejor que C. Nada mas lejos de la realidad.
Por ejemplo, el famoso cuento de que las tijeras cortan el papel, (tijeras R papel) y el papel envuelve la piedra (papel R piedra) pero... ¡Las tijeras no ganan a la piedra! Es al revés, la piedra rompe las tijeras. Este cuento despierta la curiosidad de los niños porque va en contra de la idea preconcebida de que "todo es transitivo".
Otro ejemplo, supongamos que podemos quitar toda la aleatoriedad del fútbol y que el resultado de un partido solamente dependiera de las características de los jugadores y del entrenador. Estoy personalmente convencido de que el hecho de que el Barça gane al Madrid y a su vez el Madrid gane al Atletic no conlleva que el Barça gane al Atletic. Los que suelen interesarse por las competiciones deportivas y las estrategías saben perfectamente a qué me refiero.
Un ejemplo mas sutíl es el de 3 dados un poco modificados. En vez de tener las caras habituales 1, 2, 3, 4, 5, 6 modificamos los dados para que el dado D1 tenga las caras: 1, 1, 5, 5, 5, 5 el dado D2 las caras 3, 3, 3, 4, 4, 4 y el dado D3las caras 2, 2, 2, 2, 6, 6 . Por probabilidad, resulta que el dado D1 es mejor que el dado D2 en el sentido de que suele ganar las apuestas del tipo "gana quién saca el número mayor". A su vez, por probabilidad el dado D2 gana al dado D3. Por lo tanto la situación nos lleva a pensar que D1 es un dado muy bueno y D3 un dado muy malo y por lo tanto que por probabilidad D1 gana a D3 con diferencia. Pues resulta que no es así, ¡D3 es mejor que D1! Por lo tanto si uno se dedica a realizar apuestas con estos dados modificados, basta con ofrecer al rival el lujo de elegir su dado lo cual es una aparente ventaja: "Elija usted el mejor de los 3 y si se equivoca le permitiré cambiar tantas veces como quiera". A continuación, si el rival elige D1, sabemos que hay que elegir D3, si elige D2 hay que elegir D1 y si elige D3 hay que elegir D2. Así siempre jugaremos con un dado mejor que el rival. Es la historia de las tijeras, el papel y la piedra pero bien disfrazada.
Tengo la intuición de que en la bolsa y algunas operaciones financieras con cierta complejidad, deben de existir muchas situaciones que se dan por transitivas cuando en realidad no lo son... hasta que uno se de cuenta y saque provecho de la situación ¿A que pueden volverse interesantes las matemáticas?
Relación total
Sobre un mismo conjunto E, se dice de una relación R que es total si y solo si para cualquier par de elementos e y f de E, tenemos e R f o tenemos f R e. Formalemente,
\[\forall(e,f)\in E^{2}\;\;e\,R\,f\;\;o\;\;f\,R\,e\]
En los naturales, la relación "es menor o igual a" es una relación total porque cuando tenemos dos naturales, siempre uno de los dos es menor o igual al otro.
Relación de orden
Sobre un mismo conjunto E, se dice de una relación R que es una relación de orden si y solo si es reflexiva, transitiva y antisimetrica. Si además la relación es total, obtenemos logicamente una relación de orden total y decimos que el conjunto E es totalmente ordenado por dicha relación. Así los conjuntos \(\mathbb{N},\mathbb{Z},\mathbb{Q},\mathbb{R}\) estan totalmente ordenados por la relación usual "es menor o igual a". En \(\mathbb{C}\) no disponemos de la relación de orden "es menor o igual" pero se pueden definir relaciones de orden que lo ordenan totalmente aunque desgraciadamente no seran compatibles con la estructura de cuerpo de este conjunto.
Mas adelante escribiré un articulo detallado sobre las relaciones de orden.
Relación de equivalencia
Sobre un mismo conjunto E, se dice de una relación R que es una relación de equivalencia si y solo si dicha relación es a la vez Reflexiva, Simetrica y Transitiva. Las relaciones de equivalencia juegan un papel fundamental en las matemáticas porque una relación de equivalencia divide el conjunto E en lo que se llama una Partición. Buena parte de los objetos matemáticos que se manejan se definen a partir de las Clases de Equivalencia que no son otra cosa que los elementos de una Partición.
Dada la importancia de las relaciones de equivalencia, se les dedicará una sección en esta web.
Dada la importancia de las relaciones de equivalencia, se les dedicará una sección en esta web.