Como se ha visto en la sección "Relaciones" una relación de equivalencia es una relación sobre un mismo conjunto \(E\) (es decir que relaciona entre sí los elementos de un mismo conjunto) que cumpla las tres condiciones: Reflexiva, Simetrica y Transitiva.
Las relaciones de equivalencia juegan un papel fundamental en las matemáticas porque definen una partición de \(E\). Y para poder explicar lo que es una partición veamos primero lo que son los subconjuntos y los recubrimientos.
Un conjunto \(S\) es subconjunto de \(E\) si y solo si todos sus elementos pertenecen a \(E\), decimos entonces que \(S\) está incluido en \(E\) y se nota \(S \subset E\).
\[S \subset E\;\;\Leftrightarrow\;\;\forall x\in S, x\in E\]
Sea \(P=\{S_{1},S_{2},S_{3}...\}\) una familia de subconjuntos no vacios de \(E\). \(P\) contiene una cantidad finita o infinita de elementos y cada uno de ellos es un subconjunto no vacio de \(E\).
Definimos \(I=\{1, 2, 3 ... card(P)\}\) donde \(card(P)\) designa el cardinal de \(P\), de tal forma que podemos ahora escribir:
\[P=\left\{S_{i}\right\}_{i\in I}\]
Nota: Observen que hemos supuesto implicitamente que \(P\) e \(I\) son numerables aunque sólo nos sirve para clarificar la exposición, verdaderamente no es neceario que lo sean.
Inicio
Las relaciones de equivalencia juegan un papel fundamental en las matemáticas porque definen una partición de \(E\). Y para poder explicar lo que es una partición veamos primero lo que son los subconjuntos y los recubrimientos.
Un conjunto \(S\) es subconjunto de \(E\) si y solo si todos sus elementos pertenecen a \(E\), decimos entonces que \(S\) está incluido en \(E\) y se nota \(S \subset E\).
\[S \subset E\;\;\Leftrightarrow\;\;\forall x\in S, x\in E\]
Sea \(P=\{S_{1},S_{2},S_{3}...\}\) una familia de subconjuntos no vacios de \(E\). \(P\) contiene una cantidad finita o infinita de elementos y cada uno de ellos es un subconjunto no vacio de \(E\).
Definimos \(I=\{1, 2, 3 ... card(P)\}\) donde \(card(P)\) designa el cardinal de \(P\), de tal forma que podemos ahora escribir:
\[P=\left\{S_{i}\right\}_{i\in I}\]
Nota: Observen que hemos supuesto implicitamente que \(P\) e \(I\) son numerables aunque sólo nos sirve para clarificar la exposición, verdaderamente no es neceario que lo sean.
\(P\) es un recubrimiento de \(E\) si y solo si la unión de todos sus elementos es \(E\), es decir:
\[P\;es\;un\;recubrimiento\;de\;E\;\;\Leftrightarrow\;\; \bigcup_{i\in I}S_{i}=E\]
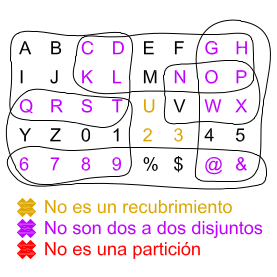
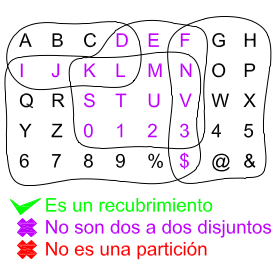



\[P\;es\;un\;recubrimiento\;de\;E\;\;\Leftrightarrow\;\; \bigcup_{i\in I}S_{i}=E\]
Dicho de otra forma, \(P\) es un recubrimiento de \(E\) si y solo si para cualquier elemento de \(E\) existe un elemento \(S\) de \(P\) que contiene dicho elemento:
\[P\;es\;un\;recubrimiento\;de\;E\;\;\Leftrightarrow\;\; \forall x\in E,\;\exists S\in P\;/\;x\in S\]
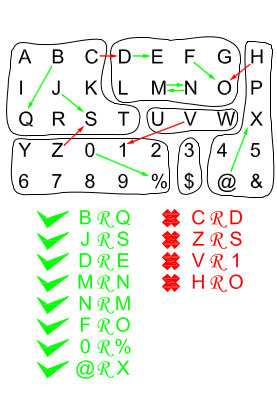
Por ejemplo, si \(E=\{A,B,C,D,E,F\}\), \(P_{1}=\{\{A,B,C,D\},\{C,D,E\},\{A,E,F\}\}\) es un recubrimiento de \(E\), pero \(P_{2}=\{\{A,B,C\},\{C,E\},\{A,E,F\}\}\) no lo es porque ningún elemento de \(P_{2}\) contiene el elemento \(D\).


A la izquierda, los elementos "U", "2" y "3" no pertenecen a niguno de los subconjutos y por lo tanto no estamos ante un recubrimiento.
En cambio a la derecha sí estamos ante un recubrimiento.
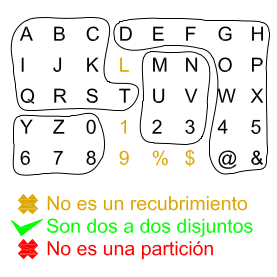
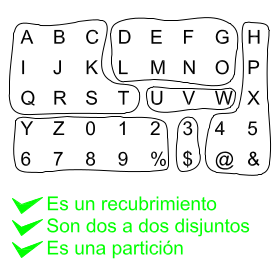
Una partición es un recubrimiento que tiene la particularidad de que ninguno de sus elementos es el conjunto vacio, y sus elementos son todos disjuntos dos a dos, es decir que la intersección entre sí de cualquier par de elementos del recubrimiento es el conjunto vacio salvo evidentemente que cojamos dos veces el mismo elemento:
\[P=\left\{S_{i}\right\}_{i\in I}\;es\;una\;partición\;de\;E\;\;\Leftrightarrow\;\;\left\{\begin{align*}&\bigcup_{i\in I}S_{i}=E\\&\forall i\in I,\;\;S_{i}\neq \emptyset\\&\forall(i,j)\in I^{2},\;i\neq j \Rightarrow S_{i} \cap S_{j}=\emptyset\end{align*}\right. \]


Como su nombre lo indica, tener una partición \(P\) de un conjunto \(E\) es establecer una "división" del conjunto \(E\) en uno o varios subconjuntos que no se solapan. Es como partir un queso.
Las particiones estan intimamente ligadas a las relaciones de equivalencia. Dada una relación \(R\) de equivalencia, para todo \(x\in E\) se define el conjunto \(\dot{x}=\{y\in E/xRy\}\) llamado "clase de equivalencia de \(x\)" y \(x\) se llama "representante" de la clase de equivalencia \(\dot{x}\). Cuando dos elementos de \(E\) pertenecen a la misma clase de equivalencia, es decir, cuando se cumple la relación \(R\) para dichos elementos, se dice de ellos que son "congruentes".

Resulta que las clases de equivalencia de una relación de equivalencia \(R\) forman una partición de \(E\). Así, a toda relación de equivalencia sobre un conjunto \(E\) le corresponde una partición de \(E\) (y una sola) y a la inversa, a toda partición de \(E\) le corresponde una relación de equivalencia sobre \(E\) (y una sola). Por lo tanto existe equivalencia (valga la redundancia) entre tener una partición de \(E\) y tener una relación de equivalencia sobre \(E\).
Demostración:1. Supongamos que tenemos una partición \(P=\left\{S_{i}\right\}_{i\in I}\) de \(E\). Definimos la relación \(R\) sobre \(E\) de forma que dos elementos cualesquiera de \(E\) están en relación si y solo si pertenecen a la misma clase, es decir:\[\forall (x,y)\in E^{2},\;\;x R y\;\Leftrightarrow\;\exists i\in I/x\in S_{i}, y\in S_{i} \]La relación así definida es:
- Reflexiva porque para cualquier elemento \(x\in E\), al ser \(P\) un recubrimiento de \(E\), existe \(i\in I / x\in S_{i}\) y se deduce de la definición de \(R\) que \(x R x\),
- Simétrica porque para todo \((x,y)\in E^2\), si \(x R y\) entonces existe \(i\in I\) tal que \(x\in S_{i}, y\in S_{i}\), lo que viene a decir que también \(y R x\).
- Transitiva porque para todo \((x,y,z)\in E^3\), si \(x R y\) y \(y R z\) entonces existe \(i\in I\) tal que \(x\in S_{i}, y\in S_{i}\) y existe \(j\in I\) tal que \(y\in S_{j}, z\in S_{j}\). Por lo tanto \(y\) pertenece tanto a \(S_{i}\) como a \(S_{j}\). Como los elementos de \(P\) son dos a dos disjuntos esto es solamente posible si \(i=j\), es decir que \(S_{i}\) y \(S_{j}\) son la misma clase. Por lo tanto hemos encontrado \(i\in I / x\in S_{i}, z\in S_{i}\) lo que viene a decir según la definición de \(R\) que \(x R z\).
Por lo tanto la relación \(R\) es una relación de equivalencia establecida de forma única a partir de la partición \(P\).2. Supongamos ahora que tenemos una relación de equivalencia \(R\) sobre un conjunto \(E\). Llamamos \(P\) al conjunto de las clases de equivalencias de \(R\).
- Puesto que \(R\) es reflexiva, \(P\) es un recubrimiento de \(E\). En efecto, cualquier elemento \(x\) de \(E\) pertenece a una clase de equivalencia por \(R\) (cuya expresión mínima sería \(\{x\}\)).
- También porque \(R\) es reflexiva, observamos que \(\dot{x}=\{y\in E/xRy\}\) contiene al menos \(x\) y por lo tanto ningúna clase de equivalencia es el conjunto vacio.
- Queda por lo tanto demostrar que si la intersección de dos elementos de \(P\) no es vacía entonces se trata de la intersección de un mismo elemento con sí mismo. Supongamos dos elementos \(S_{i}\) y \(S_{j}\) de \(P\) tales que \(S_{i}\cap S_{j} \neq \emptyset\). Luego existe \(y\in E/ y\in S_{i}, y\in S_{j}\). Sea \((x,z)\in S_{i}\times S_{j}\), \(x\) e \(y\) pertenecen a la misma clase por lo tanto \(xRy\), de la misma forma obtenemos \(zRy\). Puesto que \(R\) es simétrica obtenemos \(yRz\). Tenemos \(xRy\) y \(yRz\). Puesto que \(R\) es transitiva obtenemos \(xRz\). Cogiendo dos elementos cualesquiera de las clases \(S_{i}\) y \(S_{j}\) observamos que estos elementos pertenecen a la misma clase con lo que podemos deducir que \(S_{i}=S_{j}\).
- En esta demostración he destacado en color rojo el uso de las hipótesis. Podemos observar que para demostrar que \(R\) es una relación de equivalencia, en ningún momento se usa el hecho de que \(P\) no contiene el conjunto vacio y de hecho no es necesario. Basta con disponer de un recubrimiento cuyos elementos son dos a dos disjuntos para poder definir una relación de equivalencia \(R\). Sigue habiendo unicidad de la partición porque dicho recubrimiento no sería una partición.
Así pues, una vez tengamos sobre un conjunto \(E\) definido una relación de equivalencia \(R\), tenemos una partición de \(E\) y dicha partición se nota \(E_{/R}\) y se denomina cociente de \(E\) por la relación \(R\).
Cuando \(E\) está dotado de una determinada estructura, es decir cuando tiene leyes de composición internas o externas, lo interesante es lograr trasladar dichas leyes a un conjunto cociente. Por ejemplo, es lo que se hace para definir el conjunto de los enteros \(\mathbb{Z}\), los racionales \(\mathbb{Q}\), los reales \(\mathbb{R}\) y otros muchos conjuntos (Para los complejos \(\mathbb{C}\) el proceso es muy similar a lo que se describe a continuación aunque no es necesario cocientar).
Vamos a suponer que sobre el conjunto de objetos matemáticos \(E\) hemos definido determinada leyes internas o externas. Por ejemplo, E podría ser los naturales \(\mathbb{N}\) con las leyes usuales de adición y multiplicación. También podría ser las matrices cuadradas de dimensión n a coeficientes en \(\mathbb{R}\) con las leyes usuales de adición y multiplicación matricial. \(E\) podría ser un espacio vectorial con leyes de adición y producto externo y un largo ect.
Supongamos por ejemplo que \(E\) está dotado de las leyes \(\oplus\) y \(\otimes\). Opto por llamar usar los símbolos "\(\oplus\)" y "\(\otimes\)" en vez de los habituales "\(+\)" y "\(.\)" porque deseo destacar que no necesariamente hablo de la suma y la multiplicación entre los reales.
\[\begin{matrix}\oplus: & E^{2} & \rightarrow & E\\&(x,y) & \mapsto &x\oplus y\end{matrix}\]
\[\begin{matrix}\otimes: & E^{2} & \rightarrow & E\\&(x,y) & \mapsto &x\otimes y\end{matrix}\]
Las leyes \(\oplus\) y \(\otimes\) y otras internas o externas que se puedan definir tendrán en su caso determinadas propiedades tales como la existencia de elemento neutro, la conmutatividad, la asociatividad, distributividad una respecto a la otra etc. que hacen que \(E\) tiene un estructura de grupo, anillo, espacio vectorial, cuerpo etc.

El proceso pretende ampliar el conjunto \(E\) (para pasar de \(\mathbb{N}\) a \(\mathbb{Z}\) por ejemplo). En estos casos, empezamos por ampliar brutalmente \(E\) con un producto cartesiano sobre sí mismo: \(F=E^2\) o eventualmente un producto cartesiano entre \(E\) y \(E' \subset E\). Pero esta operación es a veces una exageración y es necesario "cocientar" el resultado \(F\) con una relación de equivalencia que va a agrupar elementos de \(F\) entre sí. Luego se busca volver a definir las leyes \(\dot{\oplus}\) y \(\dot{\otimes}\) que operan sobre el conjunto cociente\(F_{/R}\) de la misma forma que operan \(\oplus\) y \(\otimes\) sobre \(E\).
\[\begin{matrix}\dot{\oplus}: & (F_{/R})^{2} & \rightarrow & F_{/R}\\&(\dot{x},\dot{y}) & \mapsto &\dot{x}\dot{\oplus} \dot{y}\end{matrix}\]
\[\begin{matrix}\dot{\otimes}: & (F_{/R})^{2} & \rightarrow & F_{/R}\\&(\dot{x},\dot{y}) & \mapsto &\dot{x}\dot{\otimes} \dot{y}\end{matrix}\]
A la derecha se representa gráficamente una definición de \(\dot{\oplus}\) en la que simplemente se ha establecido que \(\dot{x}\dot{\oplus} \dot{y}=\dot{\overline{x \oplus y}}\), lo cual es bastante habitual si en vez de buscar ampliar \(E\) con \(F=E^{2}\) se ha escrito simplemente \(F=E\) (Ver primeros dos ejemplos abajo). Lógicamente es necesario comprobar que el resultado no depende de los representantes elegidos es decir que por ejemplo si hubieramos elegido "\(J\)" y "\(9\)" en vez de "\(K\)" y "\(\%\)", tendríamos por decir algo \(J \oplus 9=U\) y por lo tanto \(\dot{K} \dot{\oplus} \dot{\%} = \dot{J} \dot{\oplus} \dot{9} = \dot{U}=\dot{V}\).


Finalmente se establece una inyección entre \(E\) y \(F\) que a todo \(x\in E\) asocia \({x}' \in F\). Esta inyección no es sobreyectiva porque normalmente pretendemos ampliar \(E\) asimilándolo a \(F_{/R}\). Se comprueba la compatibilidad de las leyes en los conjuntos \(E\) y \(F_{/R}\) es decir que se comprueba por ejemplo que si tenemos \((x,y,z)\in E^{3}\) con \(z=x\oplus y\) tambien tendremos \(\dot{{z}'}=\dot{{x}'} \dot{\oplus} \dot{{y}'}\). Una vez las compatibilidades de este tipo se han comprobado para todas las leyes, ya no existe motivo por el que escribir "\(\dot{\oplus}\)", el cual podemos escribir "\(\oplus\)". Cuando ahora escribimos "\(x\oplus y\)", si resulta que tanto \(x\) como \(y\) pertenecen a \(E\) seguimos operandolos como siempre lo hemos hecho. Pero y si uno de los dos o ambos pertenece(n) a \(F_{/R}\) entenderemos que debemos operar en \(F_{/R}\) con la ley de composición \(\dot{\oplus}\) sustituyendo \(x\) por \(\dot{{x}'}\) y/o \(y\) por \(\dot{{y}'}\) según proceda.
Para quién no se percata del proceso de construcción usado, los elementos de \(F_{/R}\) cuyos representantes (en \(F\)) no tienen antecedentes por la inyección entre \(E\) y \(F\) aparecen como objetos nuevos salidos de la nada que vienen a completar nuestro conjunto \(E\) demasiado pequeño y se comportan muy bien con todo el mundo. Así aparecen los numeros negativos, los racionales, los reales y en cierta medida el famoso imaginario "i" de los complejos.
Ejemplo 1: Congruencia de enteros modulo \(n\)
En este ejemplo no se pretende ampliar el anillo de los enteros \(\mathbb{Z}\) sino crear un nuevo conjunto con al menos la misma estructura, e incluso lograr un cuerpo.Para este ejemplo, \(E=\mathbb{Z}\), se escoge \(F=E\), se elige un natural \(n\) no nulo y se define la relación de equivalencia \(R\):\[R:\;\;\forall (x,y) \in \mathbb{Z}^{2}, xRy \Leftrightarrow \exists k \in \mathbb{Z}\;\; /\;\; x=y+kn\]Es fácil comprobar que \(R\) es una relación de equivalencia.Cuando dos enteros \((x,y) \in \mathbb{Z}^{2}\) cumplen la relación (\(xRy\)), es decir que pertenecen a la misma clase de equivalencia, decimos que son congruentes, y se nota: \(x \equiv y\;\;\; (n)\).Se demuestra que el conjunto cociente \(\mathbb{Z}_{/R}\) es \( \{ \dot{0}, \dot{1}, \dot{2},...\dot{\overline{n-1}} \} \) el cual se nota \(\mathbb{Z}_{/n\mathbb{Z}}\).\(\mathbb{Z}_{/n\mathbb{Z}}\) es siempre un anillo, y si \(n\) es primo entonces \(\mathbb{Z}_{/n\mathbb{Z}}\) es un cuerpo usado en criptografía.
Ejemplo 2: Ángulos congruentes
Se puede leer en muchas publicaciones que dos ángulos son "congruentes" si tienen la misma medida. Pero la palabra "congruente" tiene un matiz que conviene aclarar.Hablando de ángulos orientados (positivo en un sentido y negativo en el otro), supongamos \(\alpha=\frac{3\pi}{2}\) y \(\beta=\pi\). Nos interesamos a \(\alpha+\beta=\frac{5\pi}{2}\) y nos percatamos al dibujar el ángulo que es lo mismo que dibujar un ángulo de \(\frac{\pi}{2}\). Esto es así porque se ha dado una vuelta entera (\(\frac{5\pi}{2} = \frac{\pi}{2} + 2\pi\)). Por lo tanto, \(\frac{5\pi}{2}\) y \(\frac{\pi}{2}\) son el mismo ángulo... pero no el mismo real. Hay una aparente contradicción.Los ángulos orientados pueden tomar todos los valores de \(\mathbb{R}\) (que son los reales). Pero muchos de ellos vienen a caracterizar el mismo concepto geométrico. Para poner orden en todo esto vamos a relacionar entre sí los angulos que se refieren al mismo concepto geométrico (ya tenemos nuesta relación de equivalencia) y podremos hablar de ángulos "equivalentes" o "congruentes". Así, en este ejemplo, el conjunto \(E\) es \(\mathbb{R}\) y se elige \(F=E\). Naturalmente la relación de equivalencia \(R\) viene a relacionar ángulos cuando son iguales entre sí despues de sumar o restar a uno de ellos un determinado número de vueltas enteras:\[R:\;\;\forall (x,y) \in \mathbb{R}^2, xRy \Leftrightarrow \exists k \in \mathbb{Z}\;\;/\;\; x=y+2k\pi\]Es fácil comprobar que \(R\) es una relación de equivalencia.El hecho de que dos ángulos \(\alpha\) y \(\beta\) son congruentes se ecribe \(\alpha \equiv \beta\;\;\;(2\pi)\).Cada clase de equivalencia del conjunto cociente \(\mathbb{R}_{/R}\) tiene un único representante en el intervalo \([0,2\pi)\). La clase de equivalencia se nota \(\dot{\alpha}\) y su representante \(\alpha\).\(\mathbb{R}_{/R}\) se puede dotar de forma natural de suma y multiplicación confiriendole una estructura de cuerpo:\[\begin{matrix}\dot{+}: & (\mathbb{R}_{/R})^{2} & \rightarrow & \mathbb{R}_{/R}\\&(\dot{\alpha},\dot{\beta}) & \mapsto &\dot{\alpha}\dot{+} \dot{\beta}=\dot{\overline{\alpha+\beta}}\end{matrix}\]\[\begin{matrix}\dot{\times}: & (\mathbb{R}_{/R})^{2} & \rightarrow & \mathbb{R}_{/R}\\&(\dot{\alpha},\dot{\beta}) & \mapsto &\dot{\alpha}\dot{\times} \dot{\beta}=\dot{\overline{\alpha\times\beta}} \end{matrix}\]En \(\mathbb{R}_{/R}\), podemos escribir que:\[\dot{\overline{\frac{3\pi}{2}}}\, \dot{+} \dot{\pi}=\dot{\overline{\frac{3\pi}{2}+\pi}} = \dot{\overline{\frac{5\pi}{2}}}=\dot{\overline{\frac{\pi}{2}}}\]Para simplificar, \(\dot{\alpha}\) se suele escribir \(\alpha\) y \(\dot{+}\) se suele escribir \(+\) pero cuidado porque obtenemos:\[\frac{3\pi}{2} + \pi=\frac{5\pi}{2}=\frac{\pi}{2}\]Afirmar que \(\frac{5\pi}{2}=\frac{\pi}{2}\) sería correcto siempre y cuando sabemos que estamos trabajando en \(\mathbb{R}_{/R}\) y por lo tanto afirmamos que las clases de equivalencia son iguales. Para evitar confusiones, se ecribe:\[\frac{5\pi}{2} \equiv \frac{\pi}{2} \;\;\;(2\pi)\]Es decir que nos encontramos ante ángulos congruentes modulo \(2\pi\).
Ejemplo 3: construcción de los enteros \(\mathbb{Z}\) a partir de los naturales \(\mathbb{N}\)
En este ejemplo nos proponemos ampliar el conjunto de los naturales \(\mathbb{N}\) creando los enteros \(\mathbb{Z}\). Salimos con \(E=\mathbb{N}\). Queremos definir los números negativos y para ello empezamos ampliando "exageradamente" \(E\) escribiendo \(F=E^{2}=\mathbb{N}^2\).La idea de fondo es de decir que el número "-3" es el dinero que Jaime dispone si le deben 5 euros y él debe 8 euros a los demás. Pero también es el dinero que Juan dispone si le deben 10 euros y él debe 13 euros a los demás. Por lo tanto hay que "unir" los pares \((5,8)\) y (\(10,13)\) con una relación de equivalencia ¡SIN UTILIZAR LA SUSTRACCIÓN POR SUPUESTO!
Nota: Lamentablemente hay publicaciones que hablan de "equisustractividad" y escriben "\(x-y\)" sin preocuparse de que \(x \geq y\) antes de definir los enteros. Esto significa que se definen los números negativos a partir de los números negativos. La equisustractividad es una preciosa palabreja que pone de relieve el despropósito que a buen seguro se extiende al resto de la publicación.
La relación \(R\) bien definida es la siguiente:\[R:\;\;\forall ((x,y),(z,t)) \in (\mathbb{N}^{2})^{2},\;(x,y)R(z,t)\Leftrightarrow x+t=y+z\]Así pues \((5,8)\) y (\(10,13)\) representan el mismo número negativo porque 5+13=8+10.Es muy fácil comprobar que \(R\) es una relación de equivalencia.La inyección de \(E\) en \(F\) que se usa es la aplicación que a todo \(x \in \mathbb{N}\) asigna el par \((x,0) \in \mathbb{N}^{2}\). Notese que \(\dot{\overline{(x,0)}}\) con \(x \in \mathbb{N}\) seran los enteros positivos.Escribimos \(\mathbb{Z}=(\mathbb{N}^{2})_{/R}\) y volvemos a definir la adición y la multiplicacion en \(\mathbb{Z}\) de tal forma que obtengamos la distributividad de la multiplicación respecto a la adición:\[\begin{aligned} \dot{+}: & \mathbb{Z}^{2} & \rightarrow & \mathbb{Z} \\ &(\dot{(x,y)},\dot{(z,t)}) & \mapsto &\dot{(x,y)}\dot{+} \dot{(z,t)}=\dot{\overline{(x+y,z+t)}} \\ \dot{\times}: & \mathbb{Z}^{2} & \rightarrow & \mathbb{Z} \\ &(\dot{(x,y)},\dot{(z,t)}) & \mapsto &\dot{(x,y)}\dot{\times} \dot{(z,t)}=\dot{\overline{(xz+yt,xt+yz)}} \end{aligned}\]Para dotar a \(\mathbb{Z}\) de una estructura de anillo.A partir de ahora usamos notaciones:
- "\(\dot{+}\)" se nota "\(+\)"
- "\(\dot{\times}\)" se nota "\(\times\)" o simplemente "."
- "\(\dot{(x,0)}\)" (para \(x \in \mathbb{N}\)) se nota "\(x\)"
- "\(\dot{(0,x)}\)" (para \(x \in \mathbb{N}\)) se nota "\(-x\)"
Y ya podemos trabajar en \(\mathbb{Z}\) a nuestro antojo. Jaime dispone de la misma cantidad de dinero que Juan y esta cantidad es -3 euros.
Ejemplo 4: construcción de los racionales \(\mathbb{Q}\) a partir de los enteros \(\mathbb{Z}\)
La construcción de los racionales \(\mathbb{Q}\) a partir de los enteros \(\mathbb{Z}\) es muy similar a la construcción de \(\mathbb{Z}\) a partir de \(\mathbb{N}\). Esta vez escribimos \(E=\mathbb{Z}\) y empezamos ampliando "exageradamente" \(E\) con \(F=E \times \ (E-\{0\})=\mathbb{Z} \times \mathbb{Z}^{*}\) (el segundo entero de cada par ha de ser distinto de cero).La idea es asociar los pares \((x,y) \in \mathbb{Z} \times \mathbb{Z}^{*}\) con los racionales \(\frac{x}{y}\) pero para ello hay que tener en cuenta que el par \((2x,2y)\) debe asociarse con el mismo racional pues \(\frac{2x}{2y}=\frac{x}{y}\). Por lo tanto hay que establecer una relación de equivalencia de tal forma que \((x,y)R(2x,2y)\). Dicha relación agrupará muchos pares de \(\mathbb{Z} \times \mathbb{Z}^{*}\) entre sí y nace naturalemente de lo antedicho:\[R:\;\;\forall ((x,y),(z,t)) \in (\mathbb{Z} \times \mathbb{Z}^{*})^{2},\;(x,y)R(z,t)\Leftrightarrow x.t=y.z\]Así pues \((5,8)\) y (\(10,16)\) representan el mismo racional porque 5.16=8.16. Observen que practicamente estamos haciendo lo mismo que para construir \(\mathbb{Z}\) salvo que se usa la multiplicación en vez de la adición. Sobra decir que en la definición de \(R\) no puede aparecer ninguna división.Es muy fácil comprobar que \(R\) es una relación de equivalencia, nótese no obstante que la transitividad se obtiene debido a que se trabaja en \(\mathbb{Z} \times \mathbb{Z}^{*}\), de hecho en \(\mathbb{Z}^{2}\) no la tendríamos y por lo tanto \(R\) no sería una relación de equivalencia.
Transitividad: Sean \(((x,y),(z,t),(k,q)) \in (\mathbb{Z} \times \mathbb{Z}^{*})^{3}\), si \((x,y) R (z,t)\) y \((z,t) R (k,q)\), entonces \(xt=yz\) y \(zq=tk\), se multiplica la primera igualdad por \(q\) y la segunda por \(y\) para poder deducir que \(xtq=tky\). Como \(t \neq 0\) podemos deducir \(xq=ky\) y por lo tanto \((x,y) R (k,q)\).
La inyección de \(E\) en \(F\) que se usa es la aplicación que a todo \(x \in \mathbb{Z}\) asigna el par \((x,1) \in \mathbb{Z} \times \mathbb{Z}^{*}\) (ahora usamos lógicamente el elemento neutro por la multiplicación en vez del elemento neutro por la adición como en la construcción de \(\mathbb{Z}\)). Notese que \(\dot{\overline{(x,1)}}\) con \(x \in \mathbb{Z}\) seran los racionales enteros.Escribimos \(\mathbb{Q}=(\mathbb{Z} \times \mathbb{Z}^{*})_{/R}\) y volvemos a definir la adición y la multiplicacion en \(\mathbb{Q}\) de tal forma que obtengamos coherencia con la construcción de \(\mathbb{Z}\):\[\begin{aligned} \dot{+}: & \mathbb{Q}^{2} & \rightarrow & \mathbb{Q} \\ &(\dot{(x,y)},\dot{(z,t)}) & \mapsto &\dot{(x,y)}\dot{+} \dot{(z,t)}=\dot{\overline{(xt+zy,yt)}} \\ \dot{\times}: & \mathbb{Q}^{2} & \rightarrow & \mathbb{Q} \\ &(\dot{(x,y)},\dot{(z,t)}) & \mapsto &\dot{(x,y)}\dot{\times} \dot{(z,t)}=\dot{\overline{(xz,yt)}} \end{aligned}\]Para dotar a \(\mathbb{Q}\) de una estructura de cuerpo. Notese que tanto \(\dot{\overline{(xt+zy,yt)}}\) como \(\dot{\overline{(xz,yt)}}\) pertenecen a \(\mathbb{Q}\) porque \(yt \neq 0\).A partir de ahora usamos notaciones:"\(\dot{+}\)" se nota "\(+\)""\(\dot{\times}\)" se nota "\(\times\)" o simplemente ".""\(\dot{(x,1)}\)" (para \(x \in \mathbb{Z}\)) se nota "\(x\)""\(\dot{(1,x)}\)" (para \(x \in \mathbb{Z}^{*}\)) se nota "\(x^{-1}\)""\(\dot{(x,y)}\)" (para \(x \in \mathbb{Z}\) e \(y \in \mathbb{Z}^{*}\)) se nota " \(\frac{x}{y}\) ", \(x\) se llama numerador e \(y\) se llama denomidador el cual nunca es nulo.En ningún momento hemos podido definir algo como " \(\frac{1}{0}\) " ni " \(\frac{0}{0}\) " por problemas de transitividad de \(R\). Por lo tanto no vamos a decir absolutamente nada sobre algo que no hemos definido, ni que es "infinito", ni que es "indeterminado". Si quisieramos decir algo así, primero habría que decir a qué no referimos con esto de " \(\frac{1}{0}\) " o " \(\frac{0}{0}\) " para luego aclarar qué es lo que queremos decir con que es "infinito" o "indeterminado". Otra cosa bien distinta son los cálculos de límites en los que aparecen denominadores que tienen por límite cero. En estos casos el denominador nunca se anula por lo que todo lo que se escribe tiene sentido y lo que se maneja son formas del tipo " \(\frac{1}{0}\) " y " \(\frac{0}{0}\) " que en su caso precisan estudio mas detallado para determinar el límite si lo tuviera.
Ejemplo 5: construcción de \(\mathbb{R}\) a partir de \(\mathbb{Q}\)
Será preciso volver detalladamente sobre la construcción de \(\mathbb{R}\), pero básicamente se escribe \(E=\mathbb{Q}\). Luego nos interesamos a todas las series de racionales indexadas por un natural es decir a todas las series \(u_{i \in \mathbb{N}}\) donde para cualquier \(i \in \mathbb{N}\) tenemos \(u_{i} \in \mathbb{Q}\). De todas las series posibles, \(F\) va a ser el conjunto de todas las que cumplen el criterio de Cauchy. Es decir que para cualquier serie de racionales \(u\), tenemos:\[u \in F \;\; \Leftrightarrow \;\; \forall \varepsilon \in \mathbb{Q}^{+*}, \exists n \in \mathbb{N} \;\;/\;\; (\forall (p,q) \in \mathbb{N}^{2} ,\;\; p,q>n\; \Rightarrow \;\left | u_{p}-u_{q} \right |< \varepsilon)\]Es decir que por muy pequeño que elijamos \(\varepsilon\), existirá un índice \(n\) a partir del cual todos los términos de la serie ya no se separan mas de \(\varepsilon\).En \(\mathbb{Q}\), las series que cumplan el criterio de Cauchy no son todas convergentes en \(\mathbb{Q}\).La relación \(R\) que se define sobre \(F\) es la siguiente:\[R: \;\; \forall (u,v) \in F, \;\; uRv \; \Leftrightarrow \; \lim_{n \rightarrow \infty} (u_{n}-v_{n})=0\]O lo que es lo mismo:\[R: \;\; \forall (u,v) \in F, \;\; uRv \; \Leftrightarrow \; ( \forall \varepsilon \in \mathbb{Q}^{+*}, \exists n \in \mathbb{N} \; / \; \forall p \in \mathbb{N} \;\; p>n \Rightarrow \left | u_{p}-v_{p} \right |< \varepsilon ) \]Es bastante obvio que \(R\) es una relación de equivalencia.La inyección de \(E\) en \(F\) es la aplicación que a todo racional asocia la serie constante cuyos términos son todos iguales a dicho racional. Evidentemente se trata de una serie de Cauchy.A estas alturas... ya saben que escribimos \(\mathbb{R}=F_{/R}\).Sumando y multiplicando entre sí los términos de dos series que tengan el mismo índice se puede crear una serie que es suma (respectivamente multiplicación) de las series originales y formar así un nueva serie de Cauchy (esto habría que escribirlo). Se define así la suma y la multiplicación en \(\mathbb{R}\), conjunto que pasa a tener estructura de cuerpo y en el cual todas las series de Cauchy son convergentes.