En este artículo definiremos el concepto de matriz para luego seguir hablando de suma y productos matriciales, determinantes, rango y un largo etc.
Para hacer las cosas en orden sería necesario primero estudiar los espacios vectoriales, bases, dimensiones, aplicaciones lineales etc., para luego introducir el concepto de matriz. No es lo que se hace aquí puesto que hay programas de estudio que incluyen las matrices pero no el resto de la algebra lineal.
Situémonos en un caso práctico:
Alberto, Beatriz y Catalina son tres socios de la asociación "amigos de las hortalizas". Todos los días van al mercado a comprar cada uno patatas, tomates y zanahorias para el grupo. La asociación les pide llevar las cuentas a raja tabla, así que cada día les pide lo que les ha costado a cada uno. Todos los días, los tres amigos deben entregar a la asociación tres números. Dicho de otro modo, deben entregar un vector "costes" que se define como:
\[\overrightarrow{costes}= \begin{pmatrix} a\\b\\c \end{pmatrix}\]
Donde \(a\) es el precio pagado por Alberto, \(b\) es el precio pagado por Beatriz y \(c\) es el precio pagado por Catalina. No hay necesidad de escribir una flecha encima del nombre de los vectores, pero sí que es importante escribir las coordenadas de los vectores en columna. Llamamos "vector" a este grupo de precios porque resulta que pertenece a un "espacio vectorial", y \(a\), \(b\), \(c\) son las coordenadas del vector precio escrito en la base canónica de dicho espacio vectorial. Observamos que este espacio vectorial tiene una dimensión de tres, la cual, aunque no la vayamos a definir rigurosamente en este momento, es bastante intuitivo.
Vamos de suerte porque tanto Alberto como Beatriz y Catalina tienen cada uno sus costumbres y no suelen cambiar. De hecho, cada día repiten la misma compra cada uno. Alberto compra siempre 1Kg de patatas, 1Kg de tomates y 1Kg de zanahorias, Beatriz compra siempre 3Kg de patatas y 1 Kg de zanahorias, Catalina compra 2Kg de patatas, 1 Kg de tomates y 1Kg de zanahorias:
\[\left\{\begin{matrix} \text{Alberto:}&\text{ 1 Kg de patatas,}&\text{1 Kg de tomates,}&\text{1 Kg de zanahorias} \\ \text{Beatriz:}&\text{ 3 Kg de patatas,}&\text{0 Kg de tomates,}&\text{1 Kg de zanahorias} \\ \text{Catalina:}&\text{ 2 Kg de patatas,}&\text{1 Kg de tomates,}&\text{1 Kg de zanahorias}\end{matrix}\right.\]
En cambio la mala suerte es que los precios de las hortalizas dependen del mercado y cambian cada día. Todos los días la dirección oficial del mercado de hortalizas genera un vector:
\[\overrightarrow{precios}= \begin{pmatrix} x\\y\\z \end{pmatrix}\]
Donde \(x\) es el precio en euros del kilo de patatas, \(y\) es el precio en euros del kilo de tomates y \(z\) es el precio en euros del kilo de las zanahorias.
Y observamos que dicho vector es un elemento de un espacio vectorial... de tres dimensiones sí.
Todos los días, Alberto debe calcular: \(a=1\times x+1\times y+1\times z\). Beatriz y Catalina hacen lo propio para el cálculo respectivo de \(b\) y \(c\). Entre los tres calculan las coordenadas del vector \(\overrightarrow{costes}\).
María es una intermediaría, se ofrece para echar una mano. Es una matriz. Nos permite pasar en una única operación desde el vector de precios hasta el vector de costes. Tiene forma de una tabla. La tabla "coge" un vector en un espacio de 3 dimensiones, y genera un vector en un espacio de 3 dimensiones. Luego la tabla tiene 3 columnas y 3 filas. Veamos como se las arregla María para calcular el vector \(\overrightarrow{costes}\) a partir del vector \(\overrightarrow{precios}\):
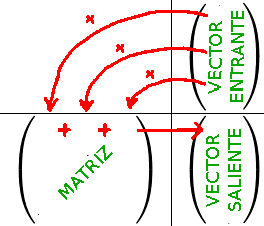

Hemos definido un producto entre matriz y vector, si no tenemos miedo de confundirlo con el producto "de toda la vida" (entre dos números), podemos escribir:
\[\overrightarrow{costes}=\text{Maria} \times \overrightarrow{precios},\;\;\; g=M \times p,\;\;\; g=Mp \]
Si a María le damos el vector: \(\overrightarrow{precios}= \begin{pmatrix} 1\\2\\3 \end{pmatrix}\) ella nos entregará el vector: \(\overrightarrow{costes}= \begin{pmatrix} 6\\6\\7 \end{pmatrix}\). Es fundamental entender las matrices como una "cosa" que coge vectores de un espacio vectorial y entrega vectores en (a priori otro) espacio vectorial. Por lo tanto una matriz caracteriza una aplicación entre dos conjuntos:

La cuestión ahora es saber... ¿Podríamos adivinar el vector \(\overrightarrow{precios}\) conociendo el vector \(\overrightarrow{costes}\)? Supongamos que un espía llamado Airam desea conocer los precios de las hortalizas con el fin de especular. Los precios se mantienen secreto pero en cambio si que logra tener acceso a las cestas de compra de Alberto, Beatriz y Catalina y sabe lo que han costado. En definitiva, conoce la matriz "María" y el vector \(\overrightarrow{costes}\). ¿Lograra deshacer lo que hizo María para obtener el vector \(\overrightarrow{precios}\)? La respuesta es bastante fácil, basta con escribir el sistema de ecuaciones siguiente, y a ver a donde nos lleva:
\[\left\{\begin{matrix} 1x&+1y&+1z&=a \\ 3x&+0y&+1z&=b \\ 2x&+1y&+1z&=c \end{matrix}\right.\]
Es un sistema lineal que se resuelve con el metodo de Gauss. No es necesario escribir siempre las variables \(x\), \(y\), y \(z\), podemos simplemente escribir:
\[ \left( \begin{array}{ ccc|c } 1 & 1 & 1 & 6 \\ 3 & 0 & 1 & 6 \\ 2 & 1 & 1 & 7 \end{array} \right) \]
Con operaciones sobre las líneas, logramos triangularizar la matriz del sistema, es decir que tenga ceros por debajo de su diagonal principal.
Paso 1 (ceros en la primera columna):
\[\begin{matrix} L_{1}\\ L_{2}-3L_{1} \\ L_{3}-2L_{1} \end{matrix} \left ( \begin{array}{ ccc | c } 1 & 1 & 1 & 6 \\ 0 & -3 & -2 & -12 \\ 0 & -1 & -1 & -5 \end{array} \right)\]
Paso 2 (cero en la segunda columna):
\[\begin{matrix} L_{1}\\ -L_{2} \\ 3L_{3}-L_{2} \end{matrix} \left ( \begin{array}{ ccc | c } 1 & 1 & 1 & 6 \\ 0 & 3 & 2 & 12 \\ 0 & 0 & -1 & -3 \end{array} \right)\]
La última línea viene a decir \(-z=-3\) con lo que ya conocemos \(z\). La segunda línea nos dará \(y\) y la primera \(x\). En este caso Airam logrará obtener el vector: \(\overrightarrow{precios}= \begin{pmatrix} 1\\2\\3 \end{pmatrix}\).
Hay una cosa muy destacable, y es que Airam está completamente seguro que estos son los precios, es decir no hay otros precios que hubieran dado los mismos costes de las cestas de compras. Airam puede ser categórico: estos son los precios que ha usado María para lograr el vector \(\overrightarrow{costes}\). Mañana los servicios de espionaje de Airam le volverán a dar otro vector de costes, y verdaderamente, poco importan las cantidades, Airam siempre logrará triangularizar la matriz María exactamente de la misma forma y de nuevo dará con los precios de forma única. Airam hace un trabajo muy parecido al de María. Se le da un vector en un espacio vectorial (el de los costes) y él entrega un vector en otro espacio vectorial (los precios). Por lo tanto sin lugar a duda Airam define una aplicación entre espacios vectoriales que no es otra que la RECIPROCA de la de María. En efecto, es recíproca porque si salimos de un vector de precios, se lo damos a María y le damos continuación el resultado a Airam volveremos a caer en el mismo vector de precios.
\[\text{Airam}=\text{María}^{-1}\]
Lo interesante es que la aplicación Airam también tiene las características de una aplicación lineal y por lo tanto al igual que María se puede escribir como matriz. Si fuéramos capaces de calcular dicha matriz, Airam sería capaz de calcular el vector \(\overrightarrow{precios}\) a partir del vector \(\overrightarrow{costes}\) en una sola operación, sin tener que triangularizar con el método de Gauss.

Al año siguiente, Alberto, Beatriz y Catalina cambiaron sus costumbres de compras. La matriz María cambió bastante pero Airam supo adaptarse sin mayor problema. Triangularizó María y todo fue sobre la seda. Así fue durante varios años hasta que un año los servicios de espionaje le entregaron a Airam unas cestas de compra muy curiosa:
\[\left\{\begin{matrix} \text{Alberto:}&\text{ 1 Kg de patatas,}&\text{1 Kg de tomates,}&\text{1 Kg de zanahorias} &\text{coste=6 euros} \\ \text{Beatriz:}&\text{ 3 Kg de patatas,}&\text{0 Kg de tomates,}&\text{2 Kg de zanahorias} &\text{coste=12 euros} \\ \text{Catalina:}&\text{ 4 Kg de patatas,}&\text{1 Kg de tomates,}&\text{3 Kg de zanahorias} &\text{coste=18 euros} \end{matrix}\right.\]
Airam empezó con sus cálculos:
\[\left ( \begin{array}{ ccc | c } 1 & 1 & 1 & 6 \\ 3 & 0 & 2 & 12 \\ 4 & 1 & 3 & 18 \end{array} \right )\]
Paso 1 (ceros en la primera columna):
\[\begin{matrix} L_{1}\\ L_{2}-3L_{1} \\ L_{3}-4L_{1} \end{matrix} \left ( \begin{array}{ ccc | c } 1 & 1 & 1 & 6 \\ 0 & -3 & -1 & -6 \\ 0 & -3 & -1 & -6 \end{array} \right)\]
Paso 2 (cero en la segunda columna):
\[\begin{matrix} L_{1}\\ -L_{2} \\ L_{3}-L_{2} \end{matrix} \left ( \begin{array}{ ccc | c } 1 & 1 & 1 & 6 \\ 0 & 3 & 1 & 6 \\ 0 & 0 & 0 & 0 \end{array} \right)\]
Caray... la última línea nos dice que \(0x+0y+0z=0\), es decir que \(0=0\) ¡Esto ya lo sabíamos! De la información \(0=0\) nunca lograremos calcular \(z\). Como mucho lo que puede hacer Airam es dar un valor cualquiera a \(z\) y con este valor calcular \(x\) y \(y\). Por ejemplo, si decide \(z=3\) logrará el vector \(\overrightarrow{precios}= \begin{pmatrix} 2\\1\\3 \end{pmatrix}\). Pero esta vez no puede estar seguro en absoluto de que este sea el vector que verdaderamente usó María. Para cada valor de \(z\) encuentra un vector de precios distinto, ¿Cual de ellos será el que usó María? No tiene manera de saberlo. Esta vez no existe ninguna aplicación recíproca.
Observemos un poco lo que ha pasado con esta nueva matriz María. Al triangularizarla hemos dado con una línea nula. Primero calculamos \(L_{2}^{(1)}=L_{2}-3L_{1}\) y \(L_{3}^{(1)}=L_{3}-4L_{1}\) y a continuación calculamos \(L_{3}^{(2)}=L_{3}^{(1)}-L_{2}^{(1)}\). Y resultó que la línea \(L_{3}^{(2)}\) es nula. Es decir que: \(0=L_{3}^{(1)}-L_{2}^{(1)}\), a saber, \(L_{3}^{(1)}=L_{2}^{(1)}\). Sustituyendo, \(L_{3}-4L_{1}=L_{2}-3L_{1}\). En definitiva, \(L_{3}=L_{2}+L_{1}\). ¡Es cierto! Si observamos de nuevo la matriz, resulta obvio que la tercera línea es suma de las dos primeras. Catalina ha traído una cesta de compras que no es otra que la suma de las cestas de Alberto y Beatriz. Y claro está... le costó lo que le ha costado a Alberto mas lo que le ha costado a Beatriz.
Airam ya no puede dar los precios de las hortalizas porque le falta información. La cesta de Catalina no le aporta ninguna información que sea pertinente, ya conocía el precio de dicha cesta conociendo el precio de las cestas de Alberto y Beatriz.
La aplicación María ya no es INYECTIVA. Hay muchos precios posibles que iban a dar los mismos costes. No es posible definir la recíproca de una aplicación que no sea inyectiva. Si varios elementos tienen la misma imagen, a partir de dicha imagen obtendríamos muchos antecedentes y no sabemos como elegir uno de ellos.

Al fin y al cabo este desastre es consecuencia directa de que \(L_{1}+L_{2}-L_{3}=0\). Observen que la desgracia de Airam no tiene que ver con lo que hayan costado las cestas. Tiene que ver con lo que contienen las cestas, es decir, con la matriz María.
Si la cesta de Catalina hubiera sido el doble de la suma de las cestas de los otros dos íbamos a tener exactamente el mismo problema al igual que si hubiera sido dos veces la de Alberto mas una vez la de Beatriz etc. En definitiva Airam será incapaz de realizar su trabajo cuando existan tres números no todos nulos \(\alpha\), \(\beta\) y \(\gamma\) tales que \(\alpha L_{1}+\beta L_{2}+\gamma L_{3}=0\). Dicho de otro modo, existe una combinación lineal de las líneas de la matriz que da la línea nula. Airam ha dado con una matriz "chunga".
Resulta pues, que existen matrices cuadradas "que se portan bien", definen aplicaciones inyectivas (además de sobreyectiva). Tienen una recíproca y todo va sobre la seda. En cambio hay matrices "chungas" en las que de alguna forma una de las líneas repite la información de las demás, o incluso no da ninguna información (línea nula). La aplicación definida por dicha matriz no es inyectiva (tampoco es sobreyectiva), y no admite recíproca.
Dada una matríz cuadrada, sería deseable poder establecer si "se porta bien" o si es "chunga". En el ejemplo que hemos visto resultaba bastante obvio que \(L_{1}+L_{2}-L_{3}=0\). Pero si la combinación lineal hubiera sido mas compleja, digamos \(77L_{1}-51L_{2}+17L_{3}=0\) ¿Quién se iba a percatar de ello? Una forma perfectamente válida es simplemente triangularizar la matriz y si damos con una línea nula es que la matriz es "chunga". Pero existe otra forma de obtener la información deseada sin triangularizar la matriz, y esto es el cálculo del determinante de dicha matriz. Lo veremos mas adelante.
Pero antes de seguir, deseo volver al asunto del espionaje de Airam. Observen que cuando los servicios de espionaje informan del contenido de las cestas y que dichas cestas definen una matriz "que se porta bien", Airam ya puede respirar tranquilo. Da igual lo que hayan costado las cestas en sí. Airam siempre será capaz de hallar los precios de las hortalizas. Pero si los contenidos de las cestas definen una matriz "chunga", la pesadilla de Airam no se limita a la matriz, también hay que preocuparse (y mucho) de lo que hayan costado las cestas. En efecto, en nuestro ejemplo en el que \(L_{3}=L_{2}+L_{1}\), es decir que la cesta de Catalina es la suma de las cestas de Alberto y Beatriz, ¿Qué hubiera pasado si los precios no siguen esta regla? Es decir que la cesta de Catalina, en vez de costar \(6+12=18\) hubiera costado \(20\) euros !!! Entonces, resulta que la información dada por los servicios de espionaje es incoherente. Es imposible que las dos primeras cestas cuesten aquello, y la tercera esto. Al triangularizar la matriz María, sí que damos con una línea nula, pero en el segundo miembro (a la derecha) obtenemos algo que no lo es. En vez de terminar con la información trivial "\(0=0\)" obtenemos en este caso "\(0=2\)". Esta vez, no es que Airam no podrá decidirse sobre los precios de las hortalizas sino que no encontrará jamás precios de las hortalizas que terminen dando "\(0=2\)", esto es imposible. Se trata de un sistema INCOMPATIBLE.
Los sistemas lineales de ecuaciones tal como el de Airam para encontrar los precios pueden ser de tres tipos:
1.- La matriz "se porta bien", no nos preocupa el segundo miembro, el sistema es determinado y tendrá una única solución de todos modos
2.- La matriz es "chunga", existe una combinación lineal de las líneas que da una linea de ceros, nos preocupa el segundo miembro
2.1 El segundo miembro "le sigue el juego" a dicha combinación lineal, el sistema es compatible-indeterminado y tiene muchas soluciones
2.2 El segundo miembro "desobedece" a la combinación lineal, el sistema es incompatible y no tiene ninguna solución
Ahora vamos a generalizar lo visto anteriormente. Alberto, Beatriz y Catalina ya no son tres amigos sino \(n\) amigos con sendas cestas de compra. Y no compran solamente tres tipos de hortalizas sino \(p\) tipos. El tabajo de Airam consiste de forma general en solucionar un sistema LINEAL de \(p\) variables \(x_{1},...,x_{p}\) y \(n\) ecuaciones que se puede escribir:
\[\left \{ \begin{array}{ ccccl } a_{11}x_{1}&+a_{12}x_{2}&...&+a_{1p}x_{p}&=b_{1}\\ a_{21}x_{1}&+a_{22}x_{2}&...&+a_{2p}x_{p}&=b_{2}\\|&|&...&|&| \\a_{n1}x_{1}&+a_{n2}x_{2}&...&+a_{np}x_{p}&=b_{n} \end{array}\right. \]
Donde los \(n\times p\) coeficientes \(a_{ij}\) son elementos de un cuerpo como \(\mathbb{R}\) o \(\mathbb{C}\) por ejemplo.
El coeficiente \(a_{ij}\) son los kilos de hortaliza del tipo "\(j\)" que podremos encontrar en la cesta de compras "\(i\)".
Buscar las soluciones a este sistema consiste en buscar los grupos de \(p\) valores \(x_{1},...,x_{p}\) que cumplen el sistema de ecuaciones. La tabla de coeficientes:
\[A=\left ( \begin{array}{ cccc } a_{11}&a_{12}&...&a_{1p}
\\ a_{21}&a_{22}&...&a_{2p}\\|&|&...&| \\a_{n1}&a_{n2}&...&a_{np} \end{array} \right ) = \left ( \begin{array}{ cc } & \begin{array}{ c } j\\ \rightarrow \end{array} \\ \downarrow i &\;\;\;\;\;a_{ij}\;\;\;\;\;\; \\ & \end{array} \right ) \]
Se denomina MATRIZ del sistema, dicha matriz es de dimensiones \(n,p\) en este orden y permite pasar de un vector de \(p\) coordenadas: \(X=\left ( \begin{array}{c} x_{1} \\ x_{2} \\|\\x_{p} \end{array} \right )\) a un vector de \(n\) coordenadas: \(B=\left ( \begin{array}{c} b_{1} \\ b_{2} \\|\\b_{n} \end{array} \right )\). El conjunto de todas las matrices posibles de dimensiones \(n,p\) y coeficientes en \(\mathbb{R}\) se escribe: \(M_{n,p}(\mathbb{R})\).
Por convención, siempre se empieza trabajando con matrices en las que \(a_{ij}\) es el coeficiente situado en la línea \(i\), columan \(j\).
Si \(n=p\) se dice que la matriz es CUADRADA.
En caso de que la matriz es cuadrada,
- \(n\) se llama el ORDEN de la matriz \(A\).
- Los coeficientes \(a_{11} , a_{22}... a_{nn}\) forman la DIAGONAL PRINCIPAL de la matriz.
- Si para todo \(i,j\in\{1..n\}\) tenemos \(a_{ij}=a_{ji}\), es decir si los términos de "cada lado" de la diagonal principal son iguales, la matriz es SIMETRICA.
- Si para todo \(i,j\in\{1..n\}\) tenemos \(a_{ij}=-a_{ji}\), es decir si los términos de "cada lado" de la diagonal principal son opuestos, la matriz es ANTISIMETRICA.
- Si para todo \(i,j\in\{1..n\}\) tenemos \(i\neq j \Rightarrow a_{ij}=0\), es decir si los términos salvo los de la diagonal principal son nulos, la matriz es DIAGONAL.
- Si para todo \(i,j\in\{1..n\}\) tenemos \(i>j \Rightarrow a_{ij}=0\), es decir si los términos por debajo de la diagonal principal son nulos, la matriz es DIAGONAL SUPERIOR.
- Si para todo \(i,j\in\{1..n\}\) tenemos \(i<j \Rightarrow a_{ij}=0\), es decir si los términos por encima de la diagonal principal son nulos, la matriz es DIAGONAL INFERIOR.
Ejemplo de matriz antisimétrica: \(\left ( \begin{array}{ccccc} 0 & 2 & -5 & 4 & 0 \\ -2&0 &1 &0 &-2 \\5 &-1 &0 &6 &5 \\ -4&0 &-6 &0 &0 \\ 0&2 &-6 &0 &0 \end{array} \right )\)
Ejemplo de matriz diagonal: \(\left ( \begin{array}{ccccc} 1 & 0 & 0 & 0 & 0 \\ 0&2 &0 &0 &0 \\0 &0 &5 &0 &0 \\ 0&0 &0 &-3 &0 \\ 0&0 &0 &0 &7 \end{array} \right )\)
Ejemplo de matriz diagonal superior: \(\left ( \begin{array}{ccccc} 1 & 3 & 5 & -1 & 1 \\ 0&2 &3 &0 &5 \\0 &0 &5 &-1 &-2 \\ 0&0 &0 &-3 &1 \\ 0&0 &0 &0 &7 \end{array} \right )\)
Ejemplo de matriz diagonal inferior: \(\left ( \begin{array}{ccccc} 1 & 0 & 0 & 0 & 0 \\ 5&2 &0 &0 &0 \\1 &2 &5 &0 &0 \\ 2&4 &-5 &-3 &0 \\ 1&3 &1 &2 &7 \end{array} \right )\)
Una consecuencia inmediata de la definición de una matriz antisemétrica es que su diagonal principal está formada de ceros. En efecto, para todo par \(i,j\in\{1..n\}\) tenemos \(a_{ij}=-a_{ji}\), en particular esto se cumple cuando \(i=j\), y en este caso tenemos: \(a_{ii}=-a_{ii}\), y por lo tanto \(a_{ii}=0\).
Los coeficientes \(b_{1}, b_{2}, ... b{n}\) forman el TERMINO INDEPENDIENTE del sistema. Se trata de un elemento de \(\mathbb{R}^{n}\). Conviene escribirlo en columna: \(\left ( \begin{array}{c} b_{1} \\ b_{2} \\|\\b_{n} \end{array} \right )\).
Podemos definir un PRODUCTO de \(M_{n,p}(\mathbb{R}) \;\times\;\mathbb{R}^{p}\) a valores en \(\mathbb{R}^{n}\), el cual dada una matriz de \(M_{n,p}(\mathbb{R}) \) asocia a todo vector de \(\mathbb{R}^{p}\) un vector en \(\mathbb{R}^{n}\):
\[ \begin{array}{ c | c } & \begin{pmatrix} x_{1} \\ | \\ x_{p} \end{pmatrix} \\ \hline \begin{pmatrix} a_{11} & - & a_{1p} \\ | & & |\\ a_{i1} & - & a_{in}\\ | & & | \\ a_{n1} & - & a_{np} \end{pmatrix} & \begin{pmatrix} \sum_{j=1}^{p}a_{1j}x_{j} \\ | \\ \sum_{j=1}^{p}a_{ij}x_{j} \\ | \\ \sum_{j=1}^{p}a_{nj}x_{j}\end{pmatrix} \end{array} \]
Con este producto, el sistema de ecuaciones incial queda reducido a:
\( A \times X = B\) que también se escribe: \( A X = B\)
Cuando se estudia un sistema de ecuaciones lineales del tipo \( A X = B\) para su resolución, pueden darse tres casos que son excluyentes entre sí:
Caso 1:
La matriz \(A\) "se porta bien". Es CUADRADA, tenemos tantas ecuaciones como incóñitas \(p = n\). somos capaces de resolver el sistema mediante el metodo de Gauss, terminamos con una matriza triangular superior, sin ninguna línea nula.
Existe una única solución \(X=\left ( \begin{array}{c} x_{1} \\ x_{2} \\|\\x_{p} \end{array} \right )\).
Si tuviéramos otro término independiente \(B\) volveríamos sistemáticamente a encontrar una nueva solución única.
La aplicación que a todo vector "de precios de hortalizas" asocia un vector de "precios de cestas" es BIYECTIVA (y puesto que es líneal, se llama isomorfismo).
Si cambiamos los precios de las cestas, volveremos a encontrar un único antecedente que son los precios de las hortalizas.
Se trata de un sistema COMPATIBLE-DETERMINADO
Caso 2:
La matriz \(A\) "es chunga". Al triangularizar con el sistema de Gauss damos con una línea nula. Hemos de preocuparnos del termino independiente.
Caso 2.1:
El termino independiente es tal que al resolver con el sistema de Gauss, en la posición que corresponde a la línea nula hemos obtenido cero. Con lo cual una de las líneas es \(0=0\) lo cual no sirve de nada y hemos de prescindir de dicha línea. Terminamos con menos ecuaciones que incógnitas. Existe infinidad de soluciones.
Podemos observar que el conjunto de las soluciones forma un espacio vectorial de dimensión \(p-n\). Es decir que si tenemos por ejemplo \(p\) incógnitas y \(n\) ecuaciones restantes ("pertinentes") o mejor dicho linealmente independientes, y \(p-n=1\), entonces las soluciones forman un espacio vectorial de dimensión uno (una recta), que podemos parametrizar con un coeficiente \(\lambda\). En cambio si \(p-n=2\) obtenemos un plano de soluciones etc.
Se trata de un sistema COMPATIBLE-INDETERMINADO
Caso 2.2:
El término independiente es tal que al resolver con el sistema de Gauss, en la posición que corresponde a la línea nula hemos obtenido algo distinto de cero. Con lo cual una de las líneas es \(0\neq0\) lo cual es imposible. El sistema no tiene soluciones.
Se trata de un sistema INCOMPATIBLE
El estudio de los determinantes nos permitirá distinguir sin recurrir al método de Gauss en qué caso nos encontramos.